Análisis de datos Experimentales por Mínimos Cuadrados

AJUSTE DE CURVAS

Uno de los objetivos en el análisis de resultados es el llegar a establecer una relación cuantitativa entre dos o más variables y mediante esta relación poder efectuar predicciones. Por lo general la relación consiste en una ecuación que expresa cómo la variable dependiente (cuyo  valor se desea predecir) es afectada por una o más variables independientes.

En esta unidad se ilustra la forma de establecer la posible relación de una variable dependiente con otra variable considerada independiente. El primer paso es disponer de una colección de datos obtenidos experimentalmente. Si se simbolizan por X y Y las variables independiente y dependiente respectivamente, y sus valores particulares por X₁, Y₁, X₂, Y₂, etc., en una tabla se dispondrían así:

X	X1	X2	X3	. . . . . . . . .	XN
Y	Y1	Y2	Y3	. . . . . . . . .	YN

 

El siguiente paso es representar los puntos (X₁, Y₁ ), (X₂, Y₂) . . . . , (X_N, Y_N) en un sistema de coordenadas rectangulares. El sistema de puntos resultantes se llama  diagrama de dispersión.

Con el diagrama de dispersión es posible representar una curva que se aproxime a los datos, es decir, que siga la tendencia de los mismos. Tal curva se llama curva de aproximación.

 En la figura 5.1 a) , por ejemplo, se ve que los datos experimentales se aproximan bien a una línea recta y se dice que entre las variables existe una relación lineal. En b), existe una relación no lineal.

Las curvas mostradas enla Fig.5.1 se denominan curvas de aproximación y  describen la tendencia de los puntos en el diagrama de dispersión. El problema general de hallar la ecuación de la curva de aproximación que se ajuste mejor al conjunto de datos con los que se obtuvo el diagrama de dispersión se denomina determinación dela CURVA DEAJUSTE.

Una curva de aproximación como la de la Fig.5.1 (a) sugiere una ecuación lineal; (ecuación de la recta) Y = a + bX; mientras que la de la curva en la Fig.5.1 (b) sugiere una ecuación cuadrática (parabólica) de la forma Y = a + bX + cX².

La dispersión de los puntos se debe a los errores que afectan en el proceso de medición tanto a la variable dependiente como a la independiente. En ocasiones puede despreciarse el error en la variable independiente al compararse con el error (o variación aleatoria) de la variable dependiente. Esto dependerá de la situación particular de las causas de error sobre cada variable al realizar el experimento.

ANÁLISIS DE REGRESIÓN

Uno de los propósitos principales de la curva de ajuste es estimar una de las variables a partir de la otra. El proceso de estimación se conoce como regresión. Si Y se va a estimar a partir de X por medio de alguna ecuación la llamamos ecuación de regresión de Y sobre X  y a la curva correspondiente curva de regresión de Y sobre X.

A continuación se presentan algunos ejemplos de relaciones denominadas funciones o ecuaciones de predicción:

Y_c  =  a + bX     (Línea Recta)

Y_c =  a + bX + cX²   (Ecuación de segundo grado o cuadrática)

Y_c = KXⁿ  o  Y_c = aX^b   (Ecuación potencial)

Y_c = A D^X  o  Y_c = a b^X (Ecuación exponencial)

En estos ejemplos, Y_c representa el valor estimado de la variable dependiente a partir del valor X, de la variable independiente.

Existen varios métodos para determinar la ecuación de regresión. El «método de mínimos cuadrados» , que se describe mas adelante, se considera el mejor; por fundamentarse en el tratamiento estadístico de los datos experimentales.

 Como se mencionó anteriormente, los errores afectan tanto a la variable independiente como a la variable dependiente, sin embargo en muy diversos casos la variable independiente puede considerarse sin error (o de error despreciable)  y considerar que la dispersión es debido unicamente a los errores en la variable dependiente. En este caso se considera que para un valor puntual de X (sin error) el valor experimental de Y se aparta del valor que predice la curva de regresión.

MÉTODO DE MÍNIMOS CUADRADOS

 Generalmente, más de una curva de un tipo dado parece  ajustarse a un conjunto de datos. Para evitar el juicio individual en la construcción de rectas, parábolas u otras curvas de aproximación, es necesario obtener una definición de la «mejor curva de ajuste», mejor parábola de ajuste,» etc

Considérese la Fig.5.2 en la cual los puntos de un conjunto de datos (hipoteticamente experimentales) se expresan por (X₁ , Y₁), (X_2,  Y₂) . . . . . (X_n, Y_n)

 Fig. 5.2  Diferencias entre los valores de la variable dependiente Y

y los de la curva de aproximación C.

 

Para un valor dado de x, por ejemplo X₁ habrá una diferencia entre el valor de Y₁ y el valor correspondiente de la curva C.

 Esta diferencia se denota por D₁  y se conoce como desviación, error, o residuo y puede ser positivo, negativo o cero. Análogamente, correspondiendo a los valores X₂ , X₃ . . . , X_N obtenemos las desviaciones D₂ , D_{3 ,}  . . .  , D_{N .}

Una medida de la «bondad de ajuste» de la curva C al conjunto de datos la suministra la cantidad D₁² + D₂² + ….. + D_N². Si la suma es pequeña el ajuste es bueno, si  es grande, el ajuste es malo.

Definición:

De todas las curvas de aproximación correspondientes a un conjunto de puntos dados, la curva que tenga la propiedad de que D₁² + D₂² + ….. + D_N²    es mínimo, se conoce como la mejor curva de ajuste.

Una curva con esta propiedad se dice que ajusta los datos por  mínimos cuadrados y se llama «Curva de regresión de mínimos cuadrados» o  simplemente «Curva de mínimos cuadrados».

Una  recta con esta propiedad se llama recta de mínimos cuadrados, una parábola con esta propiedad se llama parábola de mínimos cuadrados, etc.

REGRESIÓN LINEAL.

 Con el siguiente ejemplo se ilustra como puede tratarse un caso de regresión lineal. En la tabla siguiente se dan los resultados de 12 mediciones, las X son las cargas en miles de libras y las Y son las deflexiones correspondientes en milésimas de pulgada, en la calibración de un anillo tensor:

 

X CARGA	1	2	3	4	5	6	7	8	9	10	11	12
Y DEFLEXIÓN	16	35	45	64	86	96	106	124	134	156	164	182

 

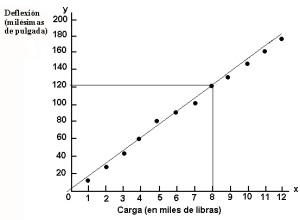
Primero se construye el diagrama de dispersión; a partir de aquí, y según la tendencia de los puntos, se traza la curva de aproximación, que resulta en la forma que se ilustra enla Fig.5.3 (línea no continua – – -).

Fig. 5.3  Gráfico de Deflexión versus carga

Es razonable suponer que la relación (curva de regresión) es lineal.

Se aplicará el método de mínimos cuadrados para determinar la ecuación de regresión. Para una relación lineal en general Y_c = a + bX ; Y_c representa el valor teórico de Y_i ó el valor estimado de Y que corresponde a un valor particular de X.

El criterio de mínimos cuadrados requiere la determinación de los valores de «a» y «b» tal que Z = Σ(Y_i – Y_c)² sea un mínimo (es decir, que tienda a cero). En la ecuación de la relación lineal «a» y «b» se denominan coeficientes de regresión: «a» es la intercepción con el eje de las ordenadas Y  y  «b» es la pendiente de la línea que mejor se ajusta.

Como se busca la recta que mejor se ajuste a los puntos experimentales, el intercepto “a” y la pendiente “b” adquieren el carácter de variables; ya que estos parametros son los que diferencian a una recta de otra.

 

Sea Z = Σ(Y_i – Y_c)² y sustituyendo  Y_c = a + bX,  Z = Σ(Y_i – a – bX)² , que debe ser un mínimo de acuerdo  a la definición de mejor curva de ajuste (en este caso, mejor recta de ajuste).

Utilizando el cálculo diferencial con derivadas parciales actuando sobre sumatorias, se llega a establecer un sistema de dos ecuaciones, denominadas ecuaciones normales para la regresión lineal o ecuaciones normales para la recta de mínimos cuadrados.

Las ecuaciones son :

 Donde n es el número de pares ordenados (X, Y) o número de puntos o número de observaciones, a y b son incógnitas que representan, como ya se mencionó, respectivamente, el intercepto y la pendiente de la recta de mínimos cuadrados.

 Para resolver estas ecuaciones se requiere obtener ΣX, ΣY, ΣXY  y  ΣX². Para el ejemplo del anillo tensor se tiene:

 

Xi	Yi	XY	X2
1	16	16	1
2	35	70	4
3	45	135	9
4	64	256	16
5	86	430	25
6	96	576	36
7	106	742	49
8	124	992	64
9	134	1206	81
10	156	1560	100
11	164	1804	121
12	182	2184	144
Σ =      78	1208	9971	650

Sustituyendo en las ecuaciones normales.

1208 = 12a +  78b

9971 = 78a + 650b

Resolviendo el sistema por el método de suma y resta, vamos a eliminar la constante «a»  multiplicando la primera ecuación por – 78 y la segunda por 12:

1208   =  12 a    +     78b    (- 78)

9971   =  78 a    +    650b    ( 12 )

*****************************************

–  94224  =-936 a    –   6084b

119652  =  936 a   +   7800b

25428  =  0       +     1716b

Para encontrar el valor de “a” sustituimos el valor de “b” en cualquiera de las ecuaciones originales; en este caso se sustituye b = 14.82 en (1):

1208  =  12a    +   78  (14.82)

1208  =  12a    +  1156

1208 – 1156  =  12a

52  =  12a

Finalmente, la ecuación de regresión queda así:

                                                  Y_c = 4.3   +  14.82 X

La línea recta que aparece cruzando el diagrama de dispersión se trazó calculando dos puntos:

P₁ (0, 4.3) y P₂ (8, 122.9) con esta ecuación, y uniendo seguidamente dichos puntos (basta con dos puntos, ya que dos puntos determinan una recta).

NOTA: Si el lector no recuerda los métodos de solución de un sistema  de ecuaciones (lo ideal sería que consultará un texto de matemática ó habrá un post de «Sistemas de Ecuaciones» si es pedido) escribiremos a continuación las fórmulas para encontrar a y b:

 Le queda al lector comprobar  estas fórmulas, deberá llegar a la misma ecuación de regresión: Y_c = 4.3  +  14.82 X. Anteriormente habíamos dicho que el valor de «a» era el intercepto con el eje de las ordenadas, Y; al observar la gráfica notamos que, efectivamente, la recta teórica corta al eje Y en la división 4.3 que es el valor que ha tomado «a»; el valor de b = 14.82 milésimas de pulgadas de  aumento en la deflexión del anillo cuando la carga x aumenta en1000 libras.

Con la ecuación calculada, podemos hacer estimaciones de Y (deflexión), y  haciendo variar el valor de X (carga). Por ejemplo, si deseamos estimar la deflexión del anillo para un valor de X = 3.5 (3500 libras); la respuesta es:

 

  Y_c = 4.3 + 14.82 (3.5) = 56.17 (milésimas de pulgada)

 Conviene aclarar que con la ecuación de regresión sólo se pueden hacer interpolaciones, ya que la ecuación expresa funcionalmente la relación de las variables, pero para pares de valores comprendidos en el dominio y rango donde se ha experimentado. En nuestro ejemplo se ha experimentado en el intervalo de1 a 12; si con la ecuación que hemos determinado, quisiéramos estimar la deflexión para una carga de20,000 libras;   X = 20, el resultado es:

Y_c = 4.3  +  14.82 (20)  = 300.7  (milésimas de pulgada).

 Este resultado es un tanto dudoso, pues lo más probable es que al aplicar una carga mayor de la que se ha experimentado el anillo tensor se deforme o hasta se rompa.

 

 REGRESIÓN CURVILÍNEA

 Función potencial o curva geométrica: Y_c = aX^b.

                                 

Aplicando  logaritmo  a  la  función  Y_c = aX^b,  tenemos:

Log Y_c  =  Log a + b Log X

Tal como hemos dicho anteriormente, la expresión S(Log Y_i – Log Y_c)² es un mínimo; sustituyendo en esta expresión Log Y_c por su valor, tenemos:

S(Log Y_i – Log a – b Log X)², es un mínimo

 Al derivar parcialmente con respecto a «a» y respecto a «b» e igualar a cero las derivadas, obtenemos las ecuaciones normales siguientes:

SLog Y = n Log a + b S Log X                         (1)

SLog X Log Y = Log a S Log X + b S(Log X)²   (2)

Ahora ajustemos una función potencial a la siguiente información, correspondiente al periodo de oscilación de un sistema resorte-masa:

m (kg)	0.20	0.40	0.60	0.80	1.00	1.20	1.40
T (s)	0.34	0.47	0.58	0.66	0.74	0.84	0.90

 

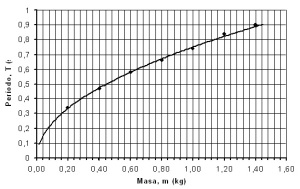
Se obtiene el diagrama de dispersión y su respectiva curva de aproximación, tal como se ilustra en la fig. 5.4 .

Fig. 5.4  Diagrama de dispersión y curva de aproximación

El diagrama de dispersión sugiere una relación de la forma T = Kmⁿ ;  en este caso, con 0 < n < 1. La ecuación se puede escribir como  T = am^b. Aplicando logaritmo a esta expresión:  Log T =  Log a + b Log m

 Las ecuaciones normales toman la forma siguiente:

SLog T = n Log a + b S Log m                                (1)

SLog m. Log T = Log a S Log m + b S (Log m)²     (2)

El siguiente cuadro contiene los valores logarítmicos necesarios para resolver las ecuaciones normales.

mi	Ti	Log m	Log T	Log m.Log T	(Log m)2	Tc
0.20	0.34	-0.69897	-0.46852	0.32748	0.48856	0.335
0.40	0.47	-0.39794	-0.32790	0.13049	0.15836	0.474
0.60	0.58	-0.22185	-0.23457	0.05248	0.04921	0.581
0.80	0.66	-0.09691	-0.18045	0.01749	0.00939	0.671
1.00	0.74	0.00000	-0.13077	0.0000	0.00000	0.750
1.20	0.84	0.07918	-0.07572	-0.00589	0.00627	0.822
1.40	0.90	0.14613	-0.04575	-0.00669	0.07135	0.887
—	S =	-1.19036	-1.46558	0.51526	0.73314	—

Sustituyendo en las ecuaciones normales se tiene:

– 1.46558 » 7 Log a  –  1.19036 b

0.51526 » – 1.19036 Log a + 0.73314 b

Resolviendo las ecuaciones se obtiene:

b = 0.50124 » 0.50

Log a = – 0.12414 de esto,   a = 0.75137 » 0.75

La ecuación de regresión es:

Log T = – 0.12414 + 0.50 Log m

 

de acuerdo a esta, se puede escribir  T = 0.75 m^0.50

Para obtener los valores teóricos de T (Tc), se utiliza esta última expresión y estos se representan en la última columna del cuadro anterior:

Ejemplo: Tc= 0.75 (0.20)^0.50 = 0.335

 

  Caso exponencial:  Y_c = a b^X

 Existen muchas transformaciones físicas en las que la variación de una magnitud en un intervalo de tiempo dado es proporcional a la cantidad de dicha magnitud al principio del intervalo. A continuación se citan varios ejemplos.

Una propiedad de las células vivas es que pueden reproducirse y así aumentar en número con el tiempo. El número de células nuevas producidas en un intervalo dado de tiempo depende del número de células presentes al principio de dicho intervalo. En otras palabras, el número de células nuevas producidas en un intervalo determinado de tiempo es proporcional al número presente.

Si la diferencia de temperatura DT entre un objeto y su medio ambiente no es demasiado grande, la rapidez de enfriamiento o de calentamiento es aproximadamente proporcional a la diferencia de temperatura entre el objeto y su medio ambiente.

En la desintegración radiactiva el cambio DN en el número de átomos padres es, para cada intervalo de tiempo Dt, proporcional al número de átomos padres presentes al comienzo del intervalo.

En los tres ejemplos anteriores, al aplicar cálculo integral, se llega a una expresión del tipo Y = a b^X , que es una relación exponencial ya que x está como exponente de una base b.Y podría representar el número de bacterias N, la diferencia de temperatura DT entre un objeto y su medio ambiente o el número de átomos padre N. La variable x representa al tiempo.

En la parte de electricidad, en un  circuito R-C en descarga encontramos la relación exponencial entre el voltaje en el capacitor y el tiempo de descarga así:

o también V = V_o (D)^t en donde se ha tomado e^-1/RC = D.

Ejemplo del caso exponencial tratado con mínimos cuadrados.

La actividad, A, de una muestra de cromo (Cr-55) medida en milicuries (mCi) a través del tiempo (en minutos) se da en la siguiente tabla:

TIEMPO, t (min)	0.0	2.5	5.0	7.5	10.0	15.0	20.0
ACTIVIDAD, A (mCi)	19.20	11.70	7.15	4.35	2.65	1.00	0.35

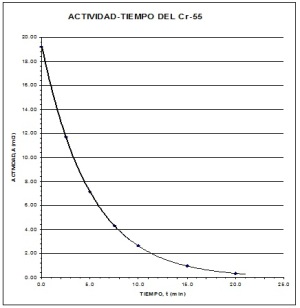
Primero representamos en una gráfica la actividad en función del tiempo para averiguar el tipo de ecuación que podría corresponderle.

 

FIG. 5.5 ACTIVIDAD-TIEMPO DEL Cr -55.

Como se observa, le corresponde el tipo de ecuación exponencial Y_c = a b^X .

A la información le ajustaremos, por mínimos cuadrados dicha función exponencial.

Aplicando logaritmos a Y_c = ab^X tenemos: Log  Y_c = Log a + X Log b.

Como en los casos anteriores, interesa minimizar la expresión:

Z = S (Log Y_i – Log a – X Log b)²

Al derivar parcialmente con respecto a «a» y «b» e igualar a cero las derivadas llegamos a las siguientes ecuaciones normales:

SLog Y_i = n Log a + Log b S X_i           (1)

S X.Log Y_i = Log a SX_i + Log b SX_i²  (2)

En este ejemplo, X representa a la variable independiente, es decir, el tiempo (t) y Y es la variable dependiente, o sea la actividad (A). El número de pares ordenados es n= 7.

Dicho lo anterior y de acuerdo a las ecuaciones normales (1) y (2), la tabla necesaria es:

t (min)	A (mCi)	log A	t*log A	t2	AC
0.0	19.20	1.283301229	0.000000000	0.00	19.36
2.5	11.70	1.068185862	2.670464654	6.25	11.76
5.0	7.15	0.854306042	4.271530209	25.00	7.14
7.5	4.35	0.638489257	4.788669427	56.25	4.34
10.0	2.65	0.423245874	4.232458739	100.00	2.64
15.0	1.00	0.000000000	0.000000000	225.00	0.97
20.0	0.35	-0.455931956	-9.118639113	400.00	0.36
S= 60.0		3.811596307	6.844483917	812.50

	Sustituyendo en (1) y (2)
	3.811596307 = 7 Log a + 60.0 Log b                  (1)
	6.844483917 = 60.0 Log a + 812.50 Log b          (2)
	Resolviendo el sistema de ecuaciones
	228.6957784 = 420 Log a + 3600 Log b			(1) * 60.0
	– 47.91138742 = – 420 Log a – 5687.5 Log b			(2) * – 7
Sumando:	180.784391 =                      – 2087.5 Log b
	Log b = 180.784391/-2087.5 = –  0.086603301
	b = (Log) – 1	-0.086603301 = 0.8192
Sustituyendo el valor de Log b en (1) y despejando:
	7 Log a = 3.811596307 – 60.0 * – 0.086603301
	Log a = 1.286827767
	a = (Log) – 1 1.286827767 = 19.36
	AC = 19.36 (0.8192)t

La expresión anterior es la ecuación de regresión.
En la última columna del cuadro anterior aparecen los valores teóricos de A_C.
Estos valores se obtuvieron utilizando la ecuación de regresión al sustituir en el exponente t los valores de la primera columna de la tabla.

Ejemplo de aplicación de ajuste de curva potencial

 

Para los datos mostrados  en la tabla siguiente :

X	1.20	1.80	3.10	4.90	5.70
Y	4.50	5.90	6.00	7.80	7.50

 

a)     Representar los datos en un diagrama de dispersión:

Fig. 5.6  Diagrama de dispersión de Y versus X 

b)  Del diagrama de dispersión, trazar la curva de aproximación

      

Fig. 5.7  Diagrama de dispersión y curva de aproximación

 de Y versus X

 

c)   Encuentre la ecuación de ajuste, asumiendo que es una potencial.

Para la curva de aproximación (potencial) Y = aX^b

Le aplicamos logaritmos: Log Y = Log a + b Log X

Las ecuaciones normales son: SLog Y = n Log a + b SLog X

SLog X Log Y = Log a SLog X + b S(Log X)²

Los datos necesarios son:

X	Y	Log X	Log Y	Log X . LogY	(Log X)2
1.20	4.50	0.079181	0.653212	0.051722	0.006269
1.80	5.90	0.255272	0.770852	0.196777	0.065164
3.10	6.00	0.491362	0.778151	0.382354	0.241437
4.90	7.80	0.690196	0.892094	0.615719	0.476371
5.70	7.50	0.755875	0.875061	0.661437	0.571347
S = 16.70	S =  31.70	S= 2.271886	S= 3.969370	S= 1.908009	S= 1.360588

 

El sistema de ecuaciones es:

3.969370 = 5 Log a + 2.271886 b

1.908009 = 2.271886 Log a + 1.360588 b

Resolviendo el sistema se tiene que:

Log a = 0.649   ,   b = 0.318

 

La ecuación de regresión es:

 

Log Yc = 0.649 + 0.318 Log X

 

                                   Por interesarnos Y_c, tomamos antilogaritmos, así:

 

Yc = 4.46 x0.318

NOTA: Las «S» significan «sumatoria.

BIBLIOGRAFÍA

BONILLA, GILDABERTO, Estadística I. Elementos de Estadística Descriptiva y Probabilidad

9ª edición, 2000. UCA Editores. El Salvador.

2.   MILLER, IRWIN Y FREUND, JOHN. Probabilidad y Estadística para Ingenieros. Primera edición. México, Editorial Reverté, 1973.

3.   MILLER, FREUND Y JOHNSON. Probabilidad y Estadística para Ingenieros.

5^a Edición. México. Prentice Hall, 1997.

4.  SPIEGEL/SCHILER/SRINIVASAN. Probabilidad y Estadística, 2ª Edición, México McGraw-Hill, 2001.

5.  SPIEGEL, MURRAY R. Estadística.  México. McGraw-Hill, 1994